《地区基尼系数与幸福感》的R代码和说明
2023-01-01
这里是对《地区基尼系数与幸福感关系的“现象核实”——基于对数据生成过程的考察》一文(《社会科学研究》2023年第1期)的一些说明。相关的Rmd文件在这里可以下载,欢迎所有人来复制和批评。
文章的缘起
由于偶然的原因,我看到了某一篇关于地区基尼系数与幸福感关系的研究,数据来源于CGSS,它利用赫希曼提出的“隧道效应”来解释其发现。我直觉地认为,这种研究不太可靠,因为地区基尼系数的估算实在是误差太大了。于是我写了一篇短文来说明这一点,并且开始投稿。结果大多数期刊都认为这只是一个无关紧要或者太过显而易见的技术细节,并不值得发表(我同意前者,这确实是一个太过显而易见的技术细节;我不同意后者,因为现实中这个技术细节正在被很多人忽视)。多数期刊并没有给我外审机会,但一位匿名评审者提醒我注意一个事实:误差只会使得系数趋近于零。
这个意见太对了。我无法解释如下现象:如果地区基尼系数的估算中误差极大,那么这只相当于是一种随机噪声,那么结果应当是两者之间不存在任何关系。毕竟我们无法用随机噪声来解释任何东西。但是我看到的文献中都确凿地发现两者之间存在关系(虽然关系的方向时而正向时而负向)。由此得到的一个可能推论是:地区基尼系数的估算虽然存在误差,但是这种误差并不是一种随机噪声,而是一种系统性偏差。这种系统性偏差诱导我们得出了某些假象性的结论。这是我后来发表的这篇文章的真正起点。我在此再次感谢那位评审者,我向他学到了很多。
关于数据的说明
我找到了CGSS2013年的数据,然后进行了如下操作,来对于常规研究进行复制。下面是所有的R代码。我使用的CGSS2013数据是从官网下载的。这个数据共有11438个记录,包括了126个区县。问卷中幸福感的测量方式如下:“总的来说,您觉得您的生活是否幸福?”选项是从“非常不幸福”到“非常幸福”的五度区分。数据中有多个有关收入的测量,我选取的是被访者的家庭收入数据(a62),而不是被访者的个人收入数据(a8a)。这是因为以前同类研究大多采取家庭收入数据。
library(pacman)
p_load(
tidyverse, haven, coefplot, MASS, lme4, ordinal, stargazer, ggrepel
)
cgss_sml <- read_stata("cgss2013_14.dta") %>%
dplyr::select(
id,
happy = a36,
income = a62,
sex = a2,
birth_y = a3a,
edu = a7a,
health = a15,
marriage = a69,
urban = vilorngh,
sheng = s41,
county = s43,
community = s45,
weight) %>%
filter(happy > 0,
income < 9999996,
birth_y > 0,
edu > 0,
edu != 14,
health > 0,
marriage > 0) %>%
mutate(
age = (2013 - birth_y) / 10,
edu_year = case_when(
edu == 1 ~ 0,
edu == 2 ~ 3,
edu <= 3 ~ 6,
edu == 4 ~ 9,
edu >= 5 & edu <= 8 ~ 12,
edu >= 9 & edu <= 10 ~ 14,
edu >= 11 & edu <= 12 ~ 16,
edu == 13 ~ 19
),
male = sex == 1,
urban = urban - 1,
spouse = marriage %in% c(2:4),
loginc = log(income + 1)
)
cat_vars <- c("sheng", "county", "community", "urban", "sex", "edu", "marriage", "spouse")
cont_vars <- c("happy", "birth_y", "age","edu_year", "income", "health", "weight")
cgss_sml <- cgss_sml %>%
mutate(across(all_of(cont_vars), as.numeric),
across(all_of(cat_vars), as_factor))
对于生成的新变量说明如下:
- age:年龄/10。之所以要除10,是为了让年龄的估计系数不会出现“0.00”这种没有信息量的显示。
- edu_year:教育年数。根据教育水平来近似估计。
- spouse:是否在婚。我们把同居、初婚有配偶、再婚有配偶三种选项合并为“在婚”,其他合并为“不在婚”。
- loginc。之所以要加一之后再进行对数,是为了把家庭收入为零者也包括在内。
然后,我计算了各个区县的收入基尼系数(gini)。在计算基尼系数时,我使用的是ineq这个包中的命令ineq。我还生成了基尼系数的平方值(gini2),以及各个区县的平均幸福感程度(happy.m)。
county <- cgss_sml %>%
group_by(sheng, county) %>%
summarise(gini = ineq::ineq(income),
gini2 = gini^2,
happy.m = mean(happy, na.rm = T),
N = n())
cgss_sml <- merge(cgss_sml, county, by=c("sheng","county"))
常规操作的复现
首先,我计算了区县基尼系数与区县被访者的幸福感均值的相关系数,结果为0.20。区县基尼系数与幸福感确实是相关的,而且在统计上非常显著。两者是正相关关系:区县基尼系数越大,幸福感的评价值越高!我还绘出了散点图,两者似乎有关系,但是没有那么直观。(为了使y轴的中文标签正过来,我使用了一个小技巧,就是先用\n把中文标签分行,然后通过设置theme(axis.title.y)把设置正过来。)
plot0 <- ggplot(data = county, aes (x= gini, y = happy.m)) +
geom_point() +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5))
plot0 + geom_smooth(method = lm, lty = 2)
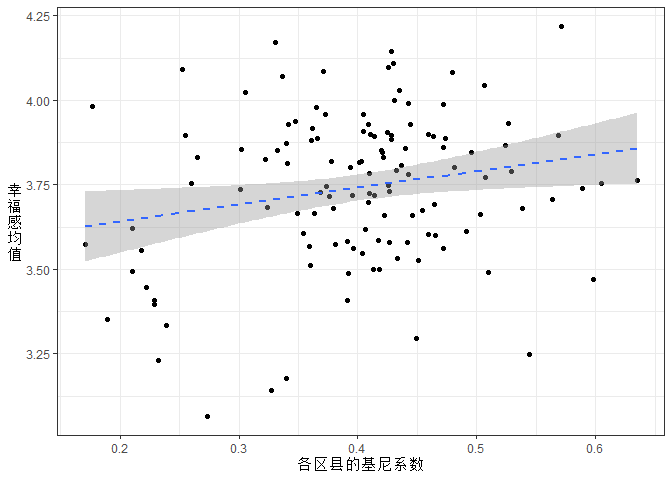
我们继续进行多元回归的分析,这样就可以在控制其他相关因素的条件下,更为准确地了解它们之间的关系。纳入如下控制变量,包括性别、年龄、受教育年限、家庭总收入的对数、居住地类型(城市/农村)、身体健康状况、当前是否有配偶,然后运行多元回归(模型1)。我没有采用通常的方式来展示回归系数结果,而是用coefplot包来将结果可视化。通常来说,这种方式能够更直观地展示结果。毕竟,面对一堆小数点,我们都会入睡的。
model1 <- lm(
happy ~ male + age + edu_year + loginc + urban + health + spouse + gini,
data = cgss_sml,
weights = weight
)
coefplot(model1, intercept = FALSE)
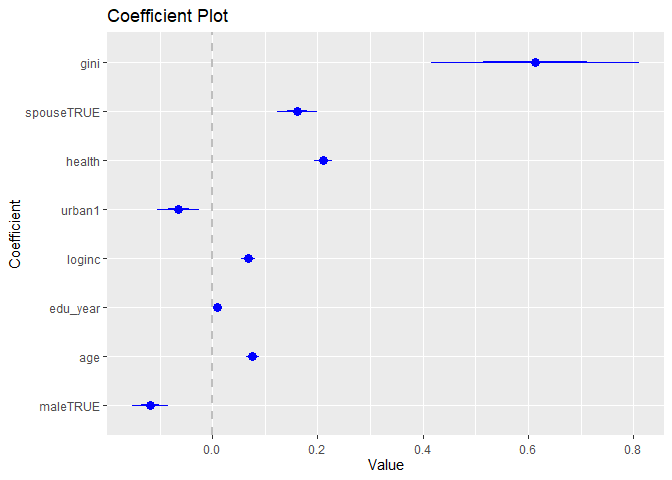
结果显示,所有的系数都是显著的。尤其是区县基尼系数的回归系数为0.6,在统计上极其显著。
- 在其余因素中,最大的影响来自于“身体健康”和“有配偶”。最小的影响是受教育年数的效应。看来上学并不能使人的幸福感有所增加。没有错,这和我们的直觉是符合的:有多少人的学校体验是如此糟糕!
- 另外一个想法是,其实基尼系数更合理的处理方法应当是除以10,因为基尼系数不可能取0和1,因此从0到1的变化程度是极其不合乎现实的;变化0.1个单位是更合乎情理的幅度。但这里不再进行修正了。
然后,我(故意地)使用了很多所谓的复杂方式,从OLS到曲线关系,然后再用ordinal logistic回归模型,再用多水平模型,最后用了多水平模型下的ordinal logistic回归模型(累积性连接混合模型)。我想说的其实是,“如果单纯以系数的统计显著性为评判指标,那么区县基尼系数与幸福感的正向关联是非常稳健的,得到了各种复杂统计模型的背书。”也就是说,如果不注意实质社会过程,复杂统计模型其实并没有能够帮到我们多少忙(这也是John Levi Martin的一个看法,我已经翻译完他的Thinking Through Statistics了,但出版仍需要一段时间)。
## 统计学家的提醒:要注意曲线关系
model2 <- lm(
happy ~ male + age + edu_year + loginc + urban + health + spouse + gini + gini2,
data = cgss_sml,
weights = weight
)
## 统计学家的批评一:你需要采用ordinal logistic回归模型。
model3 <- polr(
as.factor(happy) ~ male + age + edu_year + loginc + urban + health + spouse + gini,
data = cgss_sml,
weights = weight,
Hess = TRUE)
## 统计学家的批评二:你需要采用多水平模型。
model4 <-lmer(
happy ~ male + age + edu_year + loginc + urban + health + spouse + gini + (1|county),
data = cgss_sml,
weights = weight)
## 统计学家的建议三:采用多水平模型下的ordinal logistic回归模型。
model5 <- clmm(
as.factor(happy) ~ male + age + edu_year + loginc + urban + health + spouse + gini + (1|county),
data = cgss_sml,
weights = weight)
stargazer(model1, model2, model3, model4,
omit.stat = c("LL","ser","f"),
digits = 2,
type = "html")
| Dependent variable: | ||||
| happy | happy | happy | ||
| OLS | ordered | linear | ||
| logistic | mixed-effects | |||
| (1) | (2) | (3) | (4) | |
| male | -0.12*** | -0.11*** | -0.29*** | -0.11*** |
| (0.02) | (0.02) | (0.04) | (0.02) | |
| age | 0.08*** | 0.08*** | 0.19*** | 0.08*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| edu\_year | 0.01*** | 0.01*** | 0.02*** | 0.01*** |
| (0.002) | (0.002) | (0.01) | (0.002) | |
| loginc | 0.07*** | 0.07*** | 0.16*** | 0.07*** |
| (0.01) | (0.01) | (0.02) | (0.01) | |
| urban1 | -0.06*** | -0.06*** | -0.17*** | -0.03 |
| (0.02) | (0.02) | (0.05) | (0.02) | |
| health | 0.21*** | 0.21*** | 0.51*** | 0.21*** |
| (0.01) | (0.01) | (0.02) | (0.01) | |
| spouse | 0.16*** | 0.16*** | 0.33*** | 0.14*** |
| (0.02) | (0.02) | (0.05) | (0.02) | |
| gini | 0.61*** | 3.40*** | 1.93*** | 0.81*** |
| (0.10) | (0.54) | (0.24) | (0.19) | |
| gini2 | -3.51*** | |||
| (0.66) | ||||
| Constant | 1.54*** | 1.02*** | 1.44*** | |
| (0.10) | (0.14) | (0.12) | ||
| Observations | 9,858 | 9,858 | 9,832 | 9,858 |
| R2 | 0.10 | 0.10 | ||
| Adjusted R2 | 0.10 | 0.10 | ||
| Akaike Inf. Crit. | 25,498.98 | |||
| Bayesian Inf. Crit. | 25,578.13 | |||
| Note: | *p<0.1; **p<0.05; ***p<0.01 | |||
结果就是文章中的表1。有两点需要说明:第一,模型3中在这里的个案数为9832,这完全是由于在定序logistic中进行加权操作而造成的,真实使用的个案数其实仍然为9858,所以在论文中我仍然写为9858,以免读者误解。第二,模型5的结果无法用stargazer加工输出,所以我没有在此显示。
偏差出在什么地方?
对于数据,我最喜欢干的事情就是做图。最简单的就是散点图,散点图(的某些局部)往往能够告诉我们很多信息。这一次也不例外,我做了散点图。我想知道的是:有一些城市收入不平等程度特别高,同时人们的幸福感也特别高吗?这是哪些类型的城市?是不是通常所设想的哪些大都市地区?或者,这是因为有一些城市收入不平等程度特别低,同时人们的幸福感也特别低?这又是哪些类型的城市?是哪些经济发展更为滞后的地区吗?
CGSS2013数据不提供调查案例所在区县的具体名称,但是提供了这些区县所在的省份信息。我们绘制出了每个区县基尼系数与幸福感均值的散点图,并加入了拟合曲线。然后,我们对散点图中那些区县基尼系数小于0.3或者大于0.55的区县不再用散点表示,而是直接标注出区县所在省份。
plot1 <- plot0 +
geom_smooth(span = 1) +
ggrepel::geom_text_repel(data = county[county$gini < 0.3,], aes(label = sheng)) +
ggrepel::geom_text_repel(data = county[county$gini > 0.55,], aes(label = sheng))
plot1
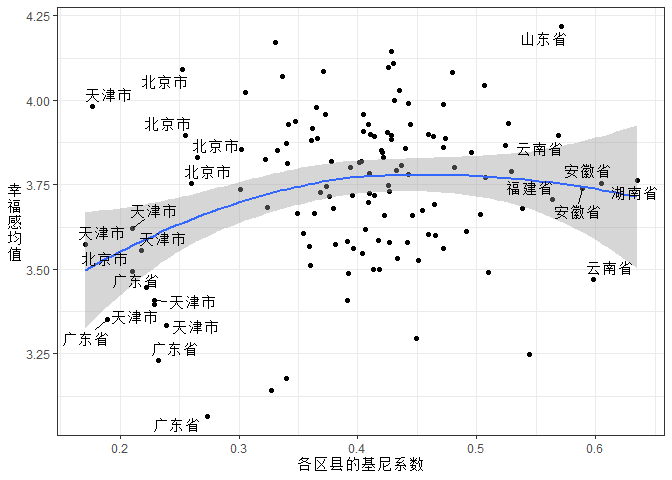
这就是图1,我发现一个与直觉认知不太相符的事实:那些基尼系数估算值低于0.3的区县大多处于北京、天津、广东省等大都市地区,基尼系数估算值高于0.55的区县却大多处于云南、湖南、安徽等相对而言并不太发达的地区。这种反常一定包含了某些信息,某些我们未曾留意过的事实。
另外,在图中可以看出,在基尼系数估算值的大部分取值范围中(大于0.3的部分),它与幸福感均值几乎不存在线性关系,拟合线近似于一条水平线。只有在散点图的左端,即当基尼系数小于0.3时,拟合线向上倾斜。左下方的一系列散点是形成这样一种拟合曲线的原因。由此看来,变量之间存在统计关联,是因为有一部分基尼系数估算值较低同时幸福感也较低的城市,而不是因为有一部分基尼系数估算值较高同时幸福感也较高的城市。
回到数据生成过程
当时我马上想到的就是,这可能与城乡有关系,可能与抽样有关系。我回到了抽样方案中,发现了其中的一些线索。在CGSS的抽样方案中,存在着必选层与抽选层的设计:
-
必选层是指那些发展处于国内领先水平的大城市。CGSS第二期调查是从直辖市、省会城市和副省级城市共36座城市中,最终选取了经济水平、教育水平及城市开放性程度综合指标最高的五个城市进行调查,分别是北京、上海、天津、广州、深圳。对于必选层中,总样本量为2000户,样本均为城市家庭户。在必选层中,街道是初级抽样单元,首先抽取40个街道,每个街道中抽取2个居委会,每个居委会抽取25个家庭户。
-
抽选层是指除去必选层市辖区以外全国所有家庭户。在抽选层中,总样本量为10000户,样本既包括城市家庭户也包括农村家庭户;区县作为初级抽样单位,首先抽取100个区县,每个区县中抽取4个居委会或村委会,每个居委会或村委会抽取25个家庭户。
-
抽选层中的区县需要进行居委会与村委会的配比。配比是根据区县城市化水平(非农人口比重)来决定的:非农人口比例在95%以上的区县,4个二级抽样单元全部是居委会;这一指标在50%-95%之间的区县,抽取3个居委会和1个村委会;指标在15%-50%之间的区县,抽取2个居委会和2个村委会;指标在15%以下的区县,抽取1个居委会和3个村委会。
在这样的抽样设计方案下,我们可以有如下推断:
-
不同类型地区的样本的城乡异质性有很大差异,而城乡异质性直接影响到测算出来的基尼系数大小。必选层中的大城市样本全部来自居委会,基尼系数因此会较小;抽选层中的区县样本中既有居委会也有村委会,基尼系数因此会较大。
-
不同类型地区的样本数量及代表性有所不同,这同样影响到测算出来的基尼系数大小。大都市地区样本的初级抽样单元为街道而不是区县,多数区县中最终仅被抽到了2个居委会(50个家庭户样本),且在同一街道;非大城市地区样本中的初级抽样单元为区县,所有区县都被抽中了4个村委会或居委会(100个家庭户样本),且在不同街道。利用地域集中程度更高、样本量更小的数据,测算出来的基尼系数当然会更低。此外,如果从严格的抽样理论上来看,大都市地区样本对区县并无代表性。
-
不同类型地区的居住隔离程度有所不同。由于城市房产价格的原因,大都市地区居住于同一居委会中的居民家庭收入往往较为接近。在农村地区,隶属于同一村委会的村民因收入提升而搬离本村庄的可能性固然存在,但相对城市而言较小。如果大城市地区存在更严重的居住隔离的情况,利用上述多阶抽样方式测算出来的基尼系数也会相对偏小。
做图进行直观验证
基于上述想法,我再次进行了直观验证:区分必选层(超大城市)与抽选层来进行数据作图。为此我必须确定每个样本是否属于必选层(处于国内领先水平的大城市)。CGSS抽样方案中说明,必选层是北京、上海、天津、广州、深圳五个城市,设计样本量为2000户,包括80个居委会。我们可能通过“省份”变量找出北京、上海、天津的样本,但广东省的样本是否只是广州与深圳两市呢?我们通过两种方式来确证这一点:第一,发现广东省的样本全部都是居委会;第二,发现北京市、上海市、天津市、广东省样本总数为1962人,与设计样本量2000户相近。因此广东省的样本就是广州与深圳两市。
我们生成了新变量big_city,来代表样本是否属于必选层(北京、上海、天津、广州、深圳)。由此我们作出了下面的新散点图,图中区分必选层与抽选层。我使用facet_wrap来分成两个小图,分别代表“必选层”和“抽选层”。
county <- county %>%
mutate(big_city =
if_else(sheng %in% c("北京市", "上海市", "天津市", "广东省"),
"大都市区",
"非大都市区"))
## 区分必选层(超大城市)与抽选层
plot2 <- ggplot(data = county, aes (x= gini, y = happy.m)) +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5)) +
geom_point() +
geom_smooth(span = 1)+
facet_wrap(~ as.factor(big_city))
plot2
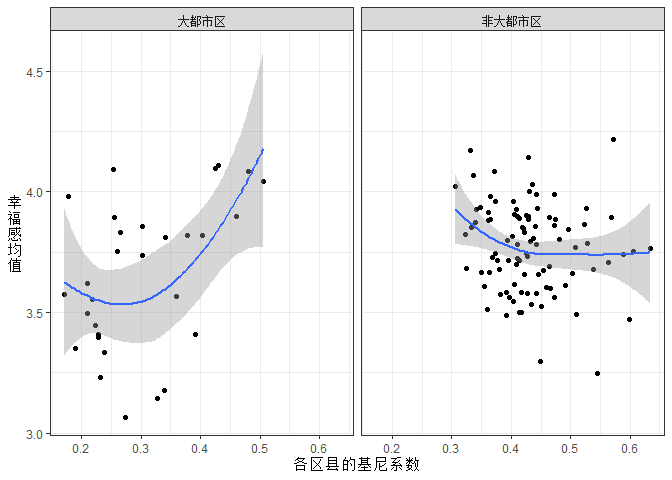
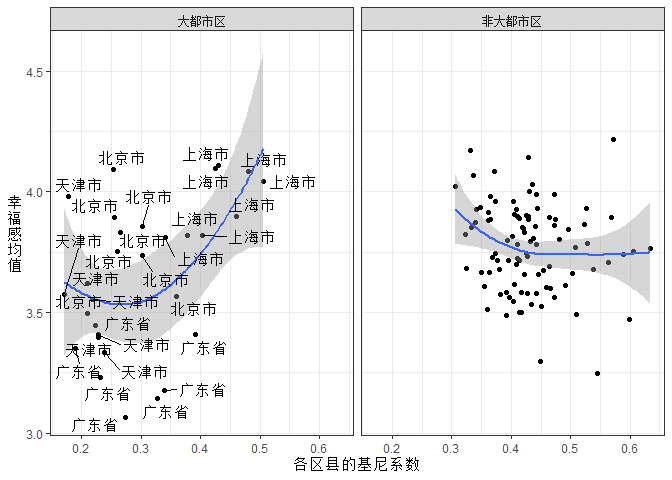
上图已经能够说明问题了。必选层的点都居于图的左边;抽选层的点都居于图的右边。必选层(大都市区)的基尼系数都比较低。分开来看以来,我们看到了更复杂的图景。我们已经开始理解所谓的曲线关系是如何出来的了。不过,必选层的图中有一点比较奇怪:大部分散点呈现出区县基尼系数与幸福感并无关系,但是右上方有一些散点使得拟合线向上翘起。这是怎么回事呢?这些散点是哪些地方?我们把必选层的散点所在省份标出来看一下。结果发现上海市极其特殊,因此将上海单独出来。
plot2 +
ggrepel::geom_text_repel(data = filter(county, big_city == "大都市区"), aes(label = sheng))
plot2_refine <- ggplot(data = county, aes (x= gini, y = happy.m)) +
geom_point(data = county[county$sheng != "上海市",],) +
geom_point(data = county[county$sheng == "上海市",], shape = 3) +
geom_smooth(data = county[county$sheng != "上海市",], span = 1) +
facet_wrap(~ as.factor(big_city)) +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5))
plot2_refine
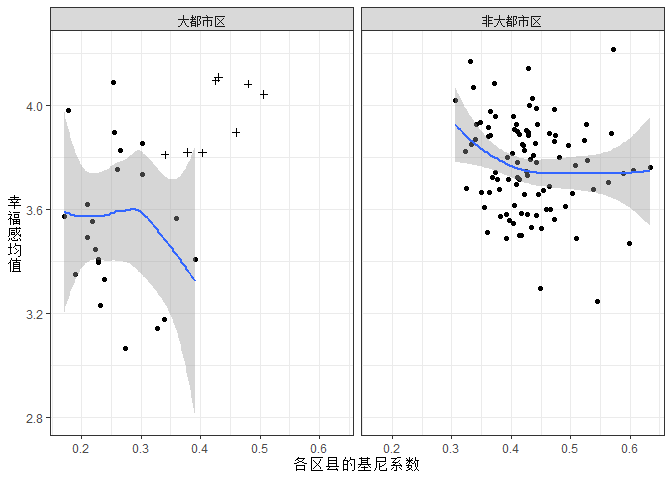
上面就是原文中的图2。我们发现大都市区中右上方的散点都是来自于上海样本(图中用十字形来代表),这些地区基尼系数估计值与幸福感均值都远高于其他都市地区。看来上海市样本在大都市地区也有特殊性,我们有必要将其作为单独对象来进行分析。在去除上海样本后,大都市地区的区县基尼系数与幸福感均值之间并不存在任何明显的相关关系。
进一步的直观验证
非大都市区中各个县区的居委会/村委会配比也是不同的。为了验证前述结论,我们可以进一步看看不同配比是否会导致基尼系数的计算出现差异。我首先生成了变量”cun_ju”来代表每个区县中“居委会/村委会配比”。
county2 <- cgss_sml %>%
group_by(county, community) %>%
summarise(is_ju = mean(urban == "1")) %>%
group_by(county) %>%
summarise(N = n(),
N_ju = sum(is_ju),
N_cun = N - N_ju,
cun_ju = paste(N_ju, N_cun, sep = "/"))
county <- merge(county, county2, by=c("county"))
我想看一下在非大都市中,村居委会配比不同的区县中基尼系数与幸福感均值的关系。
table2 <- county %>%
group_by(cun_ju) %>%
summarise(mean(gini), N = n()) %>%
filter(N>=5)
table2
| cun_ju | mean(gini) | N |
|---|---|---|
| 1/3 | 0.4464050 | 23 |
| 2/0 | 0.2985338 | 22 |
| 2/2 | 0.4409292 | 36 |
| 3/1 | 0.4063973 | 21 |
| 4/0 | 0.3644076 | 16 |
这就是文中的表2。论文中略有不同的是,把2/0和4/0那两组混合在了一起。接下来,我想了解在非大都市区中不同的居委会/村委会配比组中,地区基尼系数与幸福感均值的关系。
non_urban <- county %>%
filter(
big_city == "非大都市区",
cun_ju %in% c("1/3", "2/2", "3/1", "4/0")
)
plot3 <- ggplot(non_urban,aes (x = gini, y = happy.m)) +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5)) +
geom_point() +
facet_wrap( ~ as.factor(cun_ju), nrow = 2) +
geom_smooth(method = lm, se = FALSE)
plot3
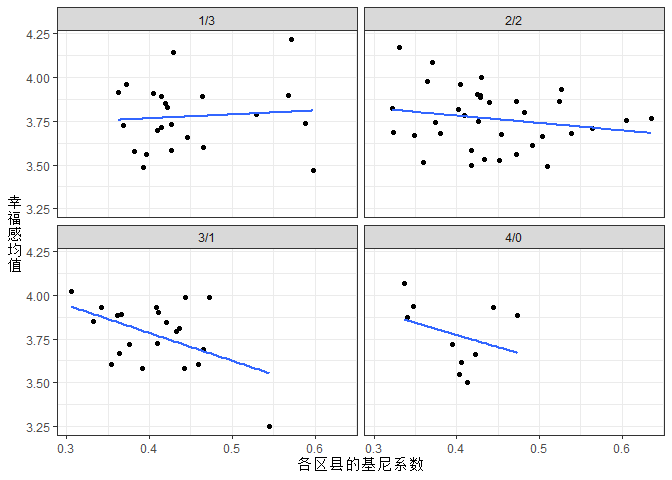
## 很明显有一个特殊点,标注出来。
plot3 <- ggplot(data = filter(non_urban, county != 68),aes (x = gini, y = happy.m)) +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5)) +
geom_point() +
geom_point(data = county[county$county == 68,], shape = 2, color = "red") + facet_wrap( ~ as.factor(cun_ju), nrow = 2) +
geom_smooth(method = lm, se = FALSE)
plot3
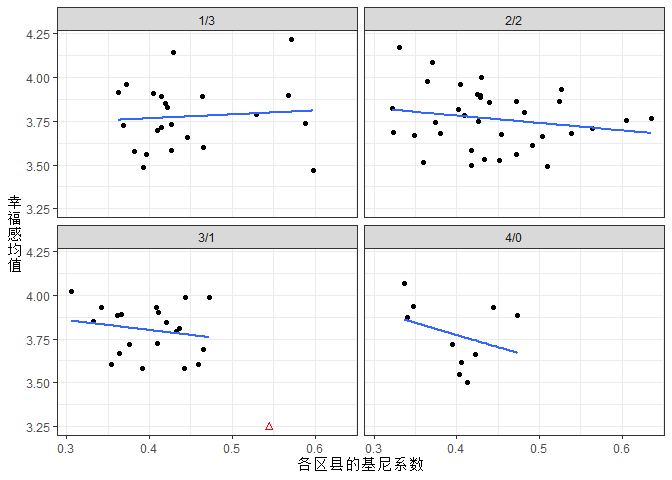
这就是文中的图3。它进一步地说明,在分组分析之后地区基尼系数与幸福感的关系极其不明显。
最后的模型分析
通过前面的作图,我们理解了偏差的重要来源——区县类型的干扰因素。
第一,模型遗漏了一项最为重要的变量——所属区县的类型 (大都市/非大都市)。这一遗漏变量与基尼系数的取值有非常强的相关关系,与幸福感之间也有较强的相关关系。我们必须把这一变量补充到模型当中,再来进行检验。
第二,在大都市样本中“上海”地区具有较为特殊的性质,它进入样本与否会使大城市地区的分析结果发生极大改变,因此我们有必要把“是否上海”作为单独变量纳入模型中,以增强模型分析的稳健性。
第三,大都市样本中在区县层面是没有代表性的,因此相对于非大都市样本而言,我们必须更为保守地对待其分析结果。
基于此,我们进行纳入了“区县类型”之后进行了新的模型分析。结果表明,无论在大都市区还是非大都市区,区县基尼系数与幸福感之间的关系在统计上都是不显著的。在区分了区县类型之后,原先的结论被否决了。事实上,一旦引入这一变量进行分组分析,区县基尼系数的效应就可能会消失或者大幅降低;区县基尼系数与幸福感之间的关系并不是稳健存在的。
## 修正后的模型分析
cgss_sml <- cgss_sml %>%
mutate(sh = sheng == "上海市",
big_city = sheng %in% c("北京市", "上海市", "天津市", "广东省"))
model6_1 <- lm(happy ~ male + age + edu_year + loginc + health + spouse + sh + gini, weights = weight, data = cgss_sml[cgss_sml$big_city == 1,])
model6_2 <- lm(happy ~ male + age + edu_year + loginc + urban + health + spouse + gini, weights = weight, data = cgss_sml[cgss_sml$big_city == 0,])
stargazer(model6_1, model6_2,
omit.stat = c("LL","ser","f"),
digits = 2,
type = "html")
| Dependent variable: | ||
| happy | ||
| (1) | (2) | |
| male | -0.16*** | -0.10*** |
| (0.04) | (0.02) | |
| age | 0.04*** | 0.08*** |
| (0.01) | (0.01) | |
| edu\_year | 0.0003 | 0.01*** |
| (0.01) | (0.003) | |
| loginc | 0.08*** | 0.07*** |
| (0.02) | (0.01) | |
| urban1 | -0.06*** | |
| (0.02) | ||
| health | 0.24*** | 0.21*** |
| (0.02) | (0.01) | |
| spouse | 0.22*** | 0.15*** |
| (0.04) | (0.02) | |
| sh | 0.30*** | |
| (0.08) | ||
| gini | 0.45 | -0.06 |
| (0.38) | (0.14) | |
| Constant | 1.41*** | 1.85*** |
| (0.29) | (0.11) | |
| Observations | 1,678 | 8,180 |
| R2 | 0.15 | 0.10 |
| Adjusted R2 | 0.14 | 0.10 |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | |
model7_1 <- clmm(as.factor(happy) ~ male + age + edu_year + loginc + health + spouse + sh + gini + (1|county), weights = weight, data = cgss_sml[cgss_sml$big_city == 1,])
model7_2 <- clmm(as.factor(happy) ~ male + age + edu_year + loginc + urban + health + spouse + gini + (1|county), weights = weight, data = cgss_sml[cgss_sml$big_city == 0,])
上面就是论文中的表3的左半部分。右半部分由于clmn的结果无法纳入到stargazer中来加工,所以没有展示出来。
一个猜想
以往文献中发现区县基尼系数与幸福感呈负向关系的研究多数采用的是CGSS2003—CGSS2006年数据,而发现区县基尼系数与幸福感呈正向关系的研究多数采用的是CGSS2010—CGSS2013年数据。为什么会有这样的规律呢?我用下图进行了一种可能性的猜测。CGSS2003—CGSS2006数据不再公开案例所在区县编码,我们无法就上述推断进行直接验证。不过,从CGSS2010—CGSS2013年数据看,这几年中大都市居民的幸福感确实有所下降。
## 用假想数据来演示基尼系数效应值方向变动不居的一种可能解释
gini_1 <- runif(30, 0.15, 0.4)
gini_2 <- runif(100, 0.3, 0.6)
x_1 <- 3 + rnorm(30, 0, 0.25)
x_2 <- 3.5 + rnorm(100, 0, 0.25)
x_3 <- 1 + x_1
gini <- c(gini_1, gini_2, gini_1, gini_2)
x <- c(x_1, x_2, x_3, x_2)
N <- c(rep(1,30), rep(2,100), rep(1,30), rep(2,100))
F <- c(rep(1,130), rep(2, 130))
da <- data.frame(gini, x, N, F)
plot4 <- ggplot() +
theme_bw() +
labs(x = "各区县的基尼系数",
y = "幸\n福\n感\n均\n值") +
theme(axis.title.y = element_text(angle = 360,vjust = 0.5)) +
geom_point(data = da, aes (x= gini, y = x, shape = as.factor(N))) +
geom_smooth(data = da, aes (x= gini, y = x, shape = as.factor(N)),method = lm, se = FALSE, lty = 2) +
geom_smooth(data = da, aes (x= gini, y = x), method = lm, se = FALSE) +
scale_shape_manual(values = c(5, 16)) +
facet_wrap(~ as.factor(F)) +
theme(legend.position = "none")
plot4
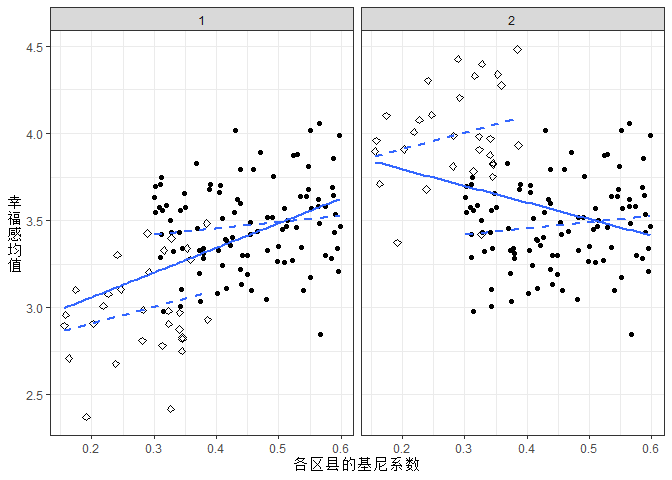
遗留的问题
我特别留意到,吴晓刚老师和李骏老师在较早的一篇相关论文中,就意识到“可能存在着未观察到的地区特征会同时影响收入不平等与人们的主观福祉”(Wu and Li,2017:53),因此构建了省级层面的面板数据来解决这种遗漏变量偏差。但是我认为,然而这种策略能够有效的前提,是面板数据分析中引入的时变变量没有遗漏;遗漏变量问题并没有因此消失,而只是转化了存在的形式。因此如果不对数据生成过程进行深入考察,面板数据分析这一统计技术也不能确保结论的可靠性。在进行面板数据分析之后,我们仍然需要去追问是哪些县市在推动变量关系得以呈现:哪些县市的收入不平等程度出现了上升,哪些县市出现了下降。
我利用 CGSS2010—2015年数据构建了省级层面的面板数据,尽管对面板数据的初始分析会呈现出统计显著的变量关系,但一旦引入地区类型变量后,就会发现变量关系至少在非大都市区中并不稳健,在大都市中的显著关系也主要起因于少数城市的特殊变化。对面板数据的分析中可能存在的偏差,我没有在文中讨论,只是在脚注中进行了一些初步说明。这仍然是一个有趣的话题。
几句闲话
我很喜欢阿博特(Andrew Abbott)在 Methods of Discovery: Heuristics for the Social Sciences中的这段话。
好多人把社会科学当成了独角戏,而非二重奏。他们眼里,社会科学就是自己的一番长篇大论之后,再抛出一个刻板的问题,现实则像旧小说里的矫情淑女,只是点头或摇头。真正的研究者不一样。他们知道,现实才不那么老实,它有层出不穷的花招,来戏弄和挑逗研究者,直觉和方法之间在不断进行交锋。社会科学实践并不是旧小说,而是现代言情剧。
我在这篇文章中写道:
那种单纯以系数的统计显著性为指引和目标的定量研究方式,看起来确实很像阿博特所戏谑的“旧小说”,尤其是它似乎不太明白,有时候现实世界这位淑女点头与摇头回应的可能根本不是自己所提出的那个问题。要真正理解点头摇头的意思,办法只能是坐下来与她进行多轮交流。
因此看来,还是现代言情剧更好玩一些?不过,对于注重仪式感的人来说,它确实太没有礼仪了。